队列

¶ 队列

队列是一种可以实现先进先出 (first in first out,FIFO) 的存储结构。与栈不一样的是，队列规定只在一端进行插入操作，在另一端进行删除操作。允许插入的一端叫做队尾 (rear)，允许删除的一端叫做队首 (front)。

¶ 分类

• 链式队列：用链表实现。

• 静态队列：用数组实现。(为了解决假溢出现象，静态队列通常都必须是循环队列)

¶ 循环队列

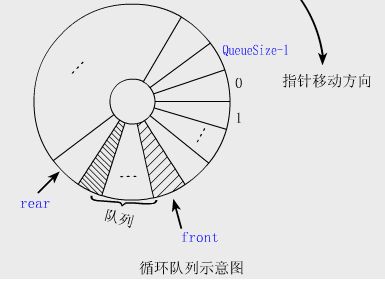
¶ 参数：front、rear

• rear 所指的单元始终为空

• 队列初始化：front 和 rear 的值都是 0。

• 队列非空：front 指向队列的第一个元素；rear 指向队列的最后一个有效元素的下一个元素。

• 队列空：front 和 rear 值相等，但不一定是 0。

¶ 算法解析

1. 入队：将值存入 rear 所代表的位置 r

• 错误写法：r=r+1

• 正确写法：r=(r+1)%数组长度

2. 出队：
f=(f+1)%数组长度

3. 判断循环队列是否为空

rear = front

4. 判断循环队列是否已满

• 多增加一个参数标志满或者空（一般不用此方式）

• 少用一个元素：如果 (r+1)%数组长度==f 表示循环队列已满

¶ 代码实现

1. 队列数据建构

typedef struct queue {
  	int *p;
  	int front;
  	int rear;
  	int maxsize;
}Queue;

2. 初始化队列

void CreateQueue(Queue *Q,int maxsize){
  	Q->p = (int*)malloc(sizeof(int)*maxsize);
  	if(!Q->p){
  		printf("Memory allocation failure!");
      	exit(-1);
	}
  	Q->front = Q->rear;
  	Q->maxize = maxsize;
}

3. 判断循环队列是否为满

int isFull(Queue *Q){
  	if ((Q->rear+1)%Q->maxsize == Q->front)
      	return 1;
  	else
      	return 0;
}

4. 判断循环队列是否为空

int isEmpty(Queue *Q){
  	if(Q->rear == Q->front)
      	return 1;
 	else
      	return 0;
}

5. 入队操作

void Enter(Queue *Q,int val){
  	if (isFull(Q)){
  		printf("The queue is full!");
  		return;
	}
  	else{
  		Q->p[Q->rear] = val;
      	Q->rear = (Q->rear+1)%Q->maxsize;
	}
}

6. 出队操作

void Delete(Queue *Q,int *val){
  	if(isEmpty(Q))
		return 0;
  	else{
  		*val = Q->p[Q->front];
      	Q->front=(Q->front+1)%Q->maxszie;
      	printf("Get out of the queue successfully!");
	}
}

7. 遍历操作

void Traverse(Queue *Q){
  	int i = Q->front;
  	printf("The items in queue are:\n");
  	while(i%Q->maxsize!=Q->rear){
  		printf("%d",Q->p[i]);
      	i=(i+1)%Q->maxsize;
	}
  	printf("\n");
}

¶ 链式队列

链式队列实现和链式栈相差不多，只是将删除操作放在了另外一端，有效的解决了顺序队列存储空间不足的缺陷。

¶ 代码实现

1. 队列节点构建

typedef struct Node{
  	int data;		//数据域
  	struct Node *next;		//指针域
}Node;

typedef struct{
  	Node *front;
  	Node *rear;
}Queue;

2. 队列初始化

int InitQueue(Queue *Q){
  	Node *head = (Node*)malloc(sizeof(Node));
  	if(!head){
  		printf("Memory allocation failed!\n");
      	return ;
	}
  	head->next = NULL;
  	Q->rear = Q->front = head;		//front和rear都指向头指针
  	printf("Init successfully!\n");
  	return 0;
}

3. 入队操作

int Enter(Queue *Q,int item){
  	Node *s = (Node*)malloc(sizeof(Node));
  	if(!s){
  		printf("Memory allocation failed!\n");
      	return ;
	}
  	s->next = NULL;
  	s->data = item;
  	Q->rear->next = s;
  	Q->rear = s;
  	return 0;
}

4. 出队操作

void Delete(Queue *Q,int *item){
  	if(Q->front == Q->rear){
  		printf("The queue is empty!\n");
      	return;
	}
  	Node *p;
  	p = Q->front->next;		//先将要出栈的节点存在P中
  	Q->front->next = p->next;		//重新构造队头元素的后继
  	*item = p->data;			//保存出队的数据；
  	if(Q->rear == p)		//判断删除的节点是否为队尾元素
      	Q->rear = Q->front;
  	free(p);
}

5. 遍历元素

void Traverse(Queue *Q){
  	if(Q->front == Q->rear){
  		printf("The queue is empty!\n");
	}
  	Node *p = Q->front->next;
  	while(p){
  		printf("%d",p->data);
      	p = p->next;
	}
  	printf("\n");
}